The code GAM numerically solves solves first order ordinary differential equations, either stiff or nonstiff in the form y'=f(x,y), with a given initial condition. The methods used are in the class of Boundary Value Methods (BVMs), namely the Generalized Adams Methods (GAMs) of order 3,5,7,9 with step size control [1,2,3,7].
![]()
![]()
The code GAM consists of three files:
- gam.f contains the main subroutines that implement the integration procedure;
- subgam.f contains subroutines used by GAM and some additional linear algebra routines;
- param.dat contains the definition of all the constants. This file must be inserted in the same directory as the main program during compilation; it is included in all the subroutine with the fortran 77 instruction include "param.dat".
If you retrieve the software, please send a message to mazzia@sun.dm.uniba.it so that we may keep you updated on any changes. Also any bug reports are appreciated.
![]()
The code has been tested on many difficult stiff test problems. For example, those contained in the test set., in Hairer's home page, or in Cash's home page. Some numerical results are summarized in [3].
To run the problems in the CWI style (release 1.0 of the IVPtestset ) it is possible to use the driver gamdo.f which contain the main program that must be compiled together with the CWI routine (release 1.0) of the problem, gam.f and subgam.f. To run the problems in the test set style (release 2.2) it is possible to use the driver gamd.f which contains the main program that must be compiled together with the test set routine of the problem, gam.f and subgam.f and the subroutine report.f . See IVP test set web page for more details.
Some of the problem have been rewritten using the CWI style (release 1.0), the routines are the following:
We report here some of the most interesting results that show the difference between the codes gam (version August 1997), radau5 by Hairer and Wanner (version July 1996)[4] and mbdfdae by Cash (version April 1997) [6]. The driver for radau5 is rad5do.f taken from CWI whereas for mbdfdae the driver is mbdfddo.f . The official links, which often direct to most recent versions, are radau5 , mbdfdae . We note that any numerical comparison is necessarily problem dependent and it also depends on the chosen evaluation parameters. Here we present the following few examples:
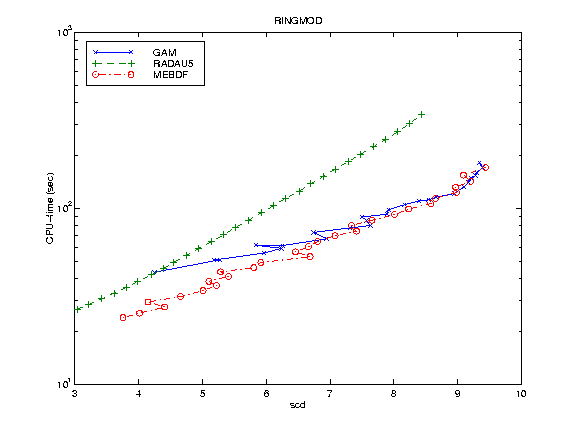
RINGMOD: the ring modulator problem with parameter cs = 2.0 x 10^{-12} which originates from electrical circuit analysis and presents solution components oscillating at very different frequencies [5];
POLLUTION: a stiff system of 20 nonlinear differential equations [5];
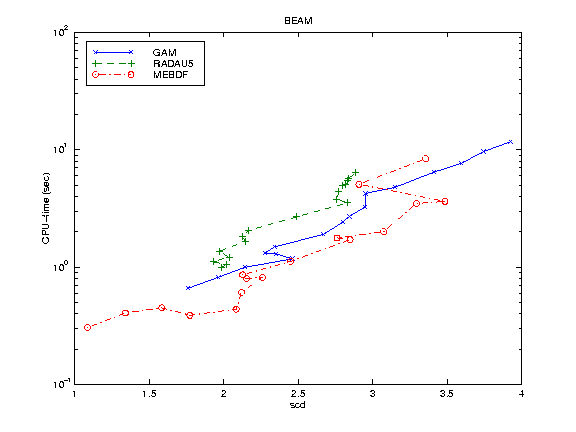
BEAM: the nonlinear elastic beam equation of dimension 80 [4];
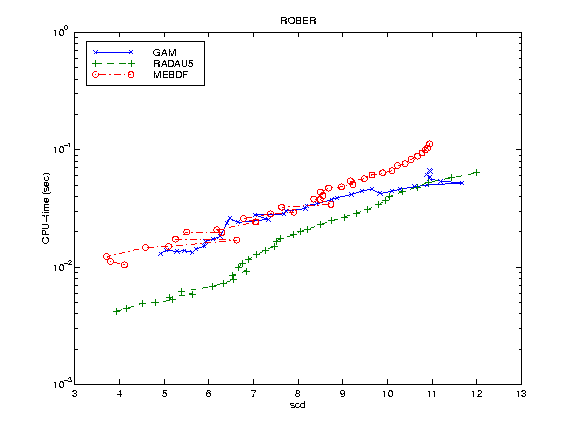
ROBER: the Robertson problem represented by a stiff system of 3 nonlinear differential equations [4];
CHEMAKZO: the Chemical Akzo Nobel problem of 6 nonlinear components [5];
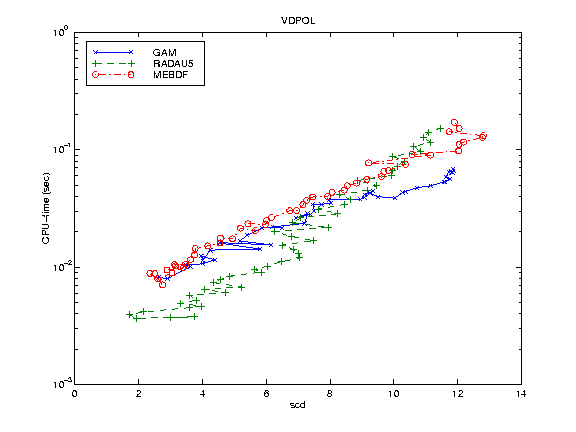
VDPOL: the Van der Pol problem of dimension 2 with parameter mu=10^3 [4];
For each numerical example we report the work precision diagram; that is, a range of input tolerances and a range of initial stepsizes were used to produce a plot of the resulting scd values (the minimum number of significant digits in the numerical solution at the endpoint) against the CPU time in seconds needed for the run. The format of these diagrams is as in [4]. Naturally this diagram strongly depends on the input tolerances and on the default parameters of each code; the variation of a parameter may considerably change the diagrams. For all problems we fixed atol=rtol and h0=rtol while the values of rtol were chosen as follows:
10^{-(6+m/4)}, m=0, ... ,28, in RINGMOD;
10^{-(3+m/4)}, m=0, ... ,44, in POLLUTION;
10^{-(2+m/4)}, m=0, ... ,16, in BEAM;
10^{-(5+m/4)}, m=0, ... ,36, in ROBER;
10^{-(7+m/4)}, m=0, ... ,28, in CHEMAKZO for RADAU5 and MEBDF, and
10^{-(4+m/4)}, m=0, ... ,40, for GAM;
10^{-(2+m/4)}, m=0, ... ,48, in VDPOL.


![]()
[2] F.IAVERNARO, F.MAZZIA, Block-Boundary Value Methods for the solution of Ordinary Differential Equations,Siam J. Sci. Comput. 21 (1) (1999) 323--339. Full paper.
[3] F.IAVERNARO, F.MAZZIA, Solving Ordinary Differential Equations by Generalized Adams Methods: properties and implementation techniques, proceedings of NUMDIFF8, Appl. Num. Math. 28 (2-4) (1998) 107-126. Full paper.
[4] E. HAIRER, G. WANNER, Solving Ordinary Differential Equations II: Stiff and Differential-Algebraic Problems, Springer Series in Computational Mathematics, vol. 14, Springer-Verlag, Berlin, 1991.
[5] W.M. LIOEN, J.J.B. DE SWART and W.A. VAN DER VEEN, Test Set for IVP Solvers, CWI, Department of Mathematics, Amsterdam, Report NM-R9615, 1996
[6] J.R.CASH, S. CONSIDINE, An MEBDF Code for Stiff Initial Value Problems, ACM Transaction on Mathematical Software, Vol 18, No. 2, 1992, pp. 142-155.
![]()